A tensor is a mathematical object that encompass scalars, vectors, and matrices, and arrays of even higher dimensions:
- 0-dimensional tensor (scalar):
123 - 1-dimensional tensor:
[1, 2, 3] - 2-dimensional tensor:
[[1, 2, 3], [4, 5, 6], [7, 8, 9]] - 3-dimensional tensor:
[[[1, 2], [3, 4]], [[5, 6], [7, 8]]] - N-dimensional tensor: …
Tensors are used to represent data like 2D images (height and width), 3D videos (height, width, and time), 4D tensor for a sequence of 3D images (height, width, depth, and time), …
They are fundamental in machine learning, particularly in deep learning, where they are used to represent data and parameters of neural networks.
Tensor etymology
The word comes from the Latin word tendere, which means “to stretch.” This is related to the original use of tensors in physics to describe physical quantities that cause stretching-like deformation materials. Over time, it came to mean it’s current mathematical abstraction.
Tensor shape
The shape tells us the size of each dimension:

Reproducing the tensors from the image with NumPy:
>>> import numpy as np
>>> np.array([[1, 2, 3, 4, 5]]).shape()
(1, 5)
>>> np.array([[1], [2], [3], [4], [5]]).shape()
(5, 1)
>>> np.array([[[1, 2, 3], [4, 5, 6]]]).shape()
(1, 2, 3)
>>> np.array([[[1], [2]], [[3], [4]], [[5], [6]]]).shape()
(3, 2, 1)
Tensor operations
The tensor datatype enables us to perform many operations such as addition, subtraction, transposition, and reshaping. Another crucial tensor operation in deep learning is the dot product, which reduces the tensor values to a single number by summing all elements. This summation is essential in calculating the activity of a neuron, where we sum all of its inputs before passing the result to an activation function.
Dot product example:
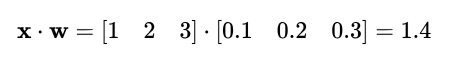
Breaking it down in smaller operations:
(1 * 0.1) + (2 * 0.2) + (3 * 0.3) =
0.1 + 0.4 + 0.9
1.4
With NumPy:
>>> import numpy as np
>>> x = np.array([1, 2, 3])
>>> w = np.array([0.1, 0.2, 0.3])
>>> print(np.dot(x, w))
1.4
Specialized libraries like CUDA enable these computations to run on the GPU, which, with its many cores and higher memory bandwidth, can perform the smaller decomposed calculations in parallel.
