Here are two things that linear algebra offers us while using matrices:
- Easing off the computation of systems of linear equations.
- Encoding vector transformations.
Let’s examine each one individually in the sections below.
A matrix can encode a system of linear equations
Solving a system of linear equations by substitution method can be laborious:
(#1) 2x - 3y + z = -20
(#2) 4x + y - 2z = 29
(#3) x + 5y + 3z = 23
(isolate x in #3) x = 23 - 5y - 3z
(substitute x in #1) -18y - 8z = -66
(substitute x in #2) -19y - 10z = -63
(rinse and repeat)
(result) x = 3, y = 7, z = -5
We can reach the solution above with less work by representing the equations as a matrix:
(from #1) [ 2 -3 1 ]
(from #2) [ 4 1 -2 ]
(from #3) [ 1 5 3 ]
Then multiply x,y,z by this matrix, and bring the right side of values of the original system of equations to our right side (-20, 29, and 23):
[ x ] [ 2 -3 1 ] [ -20 ]
[ y ] x [ 4 1 -2 ] = [ 29 ]
[ z ] [ 1 5 3 ] [ 23 ]
(some gaussian elimination goes here)
[ x ] [ 3 ]
[ y ] = [ 7 ]
[ z ] [ -5 ]
We found the same result, but much more efficiently.
A matrix can encode a vector transformation
Another incredibly clever use of matrices is to transform a vector in its vector space. Imagine your vector as an arrow and a matrix as something that can rotate, shift, tilt, mirror, scale up, or scale down that arrow of yours. Even more: a single matrix can encode n vector transformations.
Take the following 2D plane representing an image of 5x5 pixels:
□ □ ■ □ □
□ ■ □ □ □
■ □ □ □ □
□ ■ □ □ □
□ □ ■ □ □
For simplicity, pixels have only two possible values, 0 stands for empty pixel square and 1 for filled pixel square.
Now that we have the character “<” (less then), in a low 5x5 resolution font, let’s demonstrate how a matrix can flip it horizontally, making it “>” (greater then).
First, let’s refer to the reflection matrix:
[ -1 0 ]
[ 0 1 ]
This matrix flips the image horizontally, but not around the center axis of the image.
To fix this, we can use the following transformation that ‘shifts’ to the right the image to the side (by its exact width):
[ width - 1 ]
[ 0 ]
Replacing width:
[ 4 ]
[ 0 ]
Combing both transformations into a single matrix, the 2x2 flip followed by the 2x1 shift:
[ -1 0 4 ]
[ 0 1 0 ]
Time to apply it on the x,y values of the image:
[ new x ] [ x ] [ -1 0 4 ]
[ new y ] = [ y ] x [ 0 1 0 ]
[ 1 ] [ 1 ] [ 0 0 1 ]
new x = -1x + 0y + 4 = -x + 4
new y = 0x + 1y + 0 = y
Notice how handy it was to make it a triple by appending 1. The constant 1 acts as ‘just add this number’ (+4 to x in our example). This third coordinate we just added is called “homogeneous”.
Multiplying a pixel from the original image by this matrix gives the new pixel location on the new flipped image. Do it for all pixels and you’ll get the expected “>”:
□ □ ■ □ □
□ □ □ ■ □
□ □ □ □ ■
□ □ □ ■ □
□ □ ■ □ □
Flipping an image file
Let’s perform the same vertical flipping but this time on an image file, by using Python. Our input will be this image of a hand pointing left:
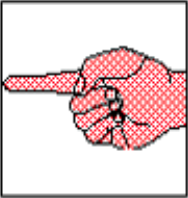
Encoding the image as PPM image format (Portable Pixmap Format) will make our life easier. The file format couldn’t be simpler: it encodes exact pixel values without compression.
Converting our file to .ppm:
$ convert pointing-left.png pointing-left.ppm
The script that flips it:
from imageio.v2 import imread, imwrite # pip install imageio
import numpy as np # pip install numpy
def flip_horizontal(input_pixels):
# image height and width in pixels
height, width, _ = input_pixels.shape
# declaring our 'flip then shift' transformation matrix
matrix_row_1 = [-1, 0, width - 1]
matrix_row_2 = [0, 1, 0]
matrix_row_3 = [0, 0, 1]
np_matrix = np.array([ matrix_row_1, matrix_row_2, matrix_row_3 ])
# all possible x,y coordinate
coordinates = np.array([[x, y, 1] for y in range(height) for x in range(width)])
# apply the transformation matrix to the coordinates
flipped_coordinates = coordinates @ np_matrix.T
# declaring the output pixels
output_pixels = np.zeros_like(input_pixels)
# Map the pixels to their new positions
for (x, y, _), (new_x, new_y, _) in zip(coordinates, flipped_coordinates):
output_pixels[new_y, new_x] = input_pixels[y, x]
return output_pixels
if __name__ == '__main__':
# load the input image
input_pixels = imread('pointing-left.ppm')
# perform the flip
output_pixels = flip_horizontal(input_pixels)
# save the flipped image as output
imwrite('pointing-right.ppm', output_pixels, format='PPM')
print(f'Flipped image saved succesfully')
Run it and you should have the resulting image, pointing to the right:
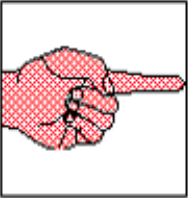
It’s important to point out that the example above is just illustrative, in reality it is much easier to rely on NumPy’s slicing:
flipped_pixels = pixels[:, ::-1, :]
