A norm defines the magnitude of a vector in the vector space. The most commonly used norms are L1 and L2 (but there are many others). Their formula is fairly simple, but what about the intuition behind it? That’s what we will see in this article.
Ah, and before we go, note that ||x|| (double bars) is a notation meaning “norm of x”.
Lp norm
Both L1 and L2 are derived from the Lp norm:
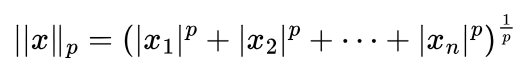
or
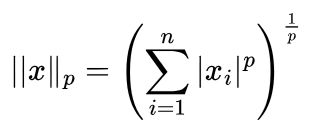
The Lp norm is a general function that extends measuring distances beyond the familiar Euclidean distance. Change “p” and you have a new norm!
L1 norm
Now that we just saw Lp norm in the section below it’s easy to define L1: Lp norm where p = 1.
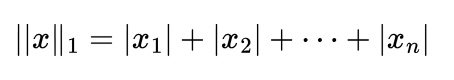
or
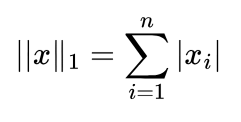
Basically, you just sum all vector components. Take the following (3,2) point as example, in the cartesian plane:
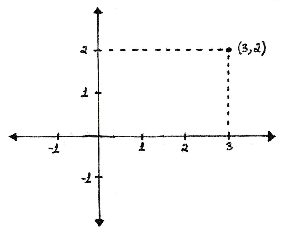
Its L1 distance is 5 (3+2). But why?
Imagine a city with perfectly squared blocks. Let’s travel from corner (0,0) to corner (3,2):
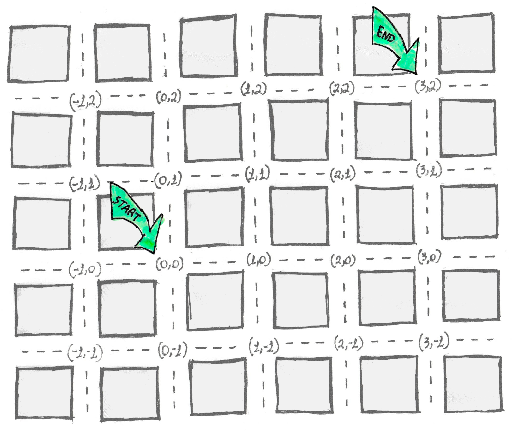
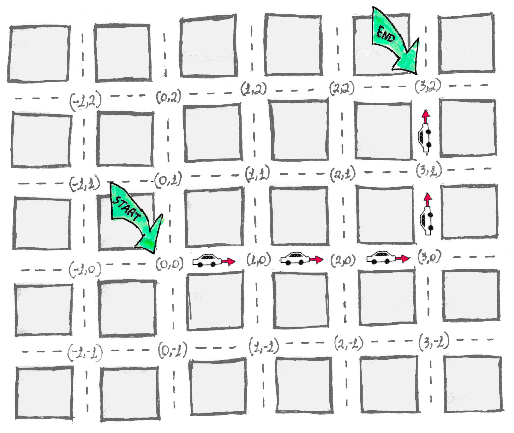
By using a car, we can go east then north (horizontal then vertical in the 2D plane):
Or north then east (vertical then horizontal in the 2D plane):
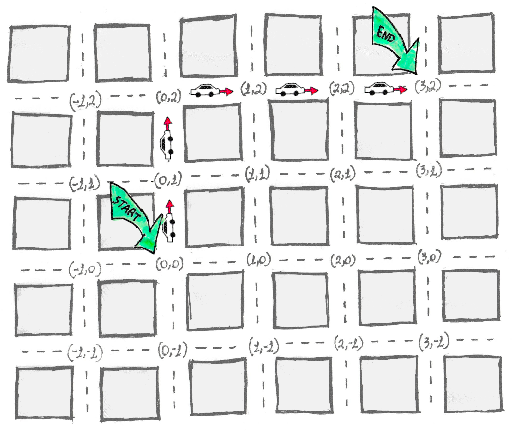
We can turn at every corner (making a ’ladder’ shape in the 2D plane):
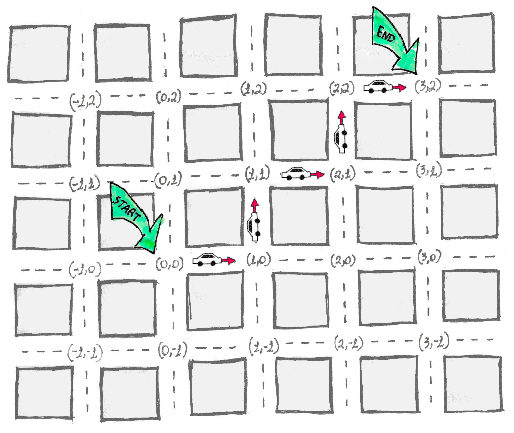
In any of the examples, count how many blocks the car has traveled. It’s always 5 (3+2) no matter the route.
This is the reason why L1 is sometimes called “Manhattan distance” or even “taxicab distance”.
L2 norm
Similar to L1, L2 is the Lp norm where p = 2.
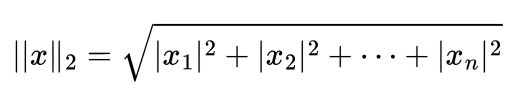
or
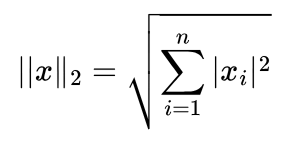
If L1 is like a car, L2 is like a helicopter traveling in a perfect diagonal, going over the buildings:
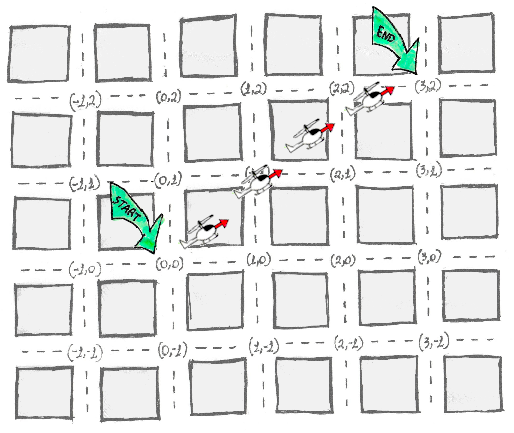
Which forms a triangle:
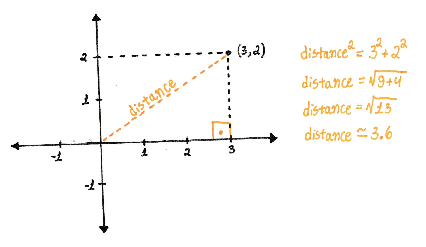
It’s not a coincidence, L2 is just Pythagoras’ theorem (square root of 3²+2² = 3.16). This is the “Euclidean distance”.
