A vector space can be a Euclidean space, but it isn’t one by definition. Let’s explore what that means in the sections below.
Word of warning: these are notes from a linear algebra beginner, please consult your local mathematician before referring to anything from this article!
‘Pure’ vector space
A vector space by itself, without additional bells and whistles, it is not a Euclidean space. Their eight axioms are not sufficient to derive a geometrical relationship between the vectors.
(below, “u” and “v” are vectors, “λ” and “ξ” are scalars)
Vector addition axioms:
- Neutral addition:
u + 0 = u - Additive inverse:
u + (-u) = 0 - Commutativity:
u + v = v + u - Associativity:
(u + v) + w = u + (v + w)
Vector multiplication by scalars axioms:
- Neutral multiplication:
1 * u = u - Associativity over multiplication:
λ * (ξ * u) = (λ * ξ) * u - Distributivity over scalar addition:
u * (λ + ξ) = (u * λ) + (u * ξ) - Distributivity over vector addition:
λ * (u + v) = (λ * u) + (λ * v)
The vectors in such space move accordingly to the rules of vector addition and scalar multiplication. The only thing resembling a ‘metric’ in this space is the vector definition itself. Distances between vectors are measured, well, in vector.
No inherent geometrical relationship exists here. We have to bring something else to have lengths and angles.
Norm
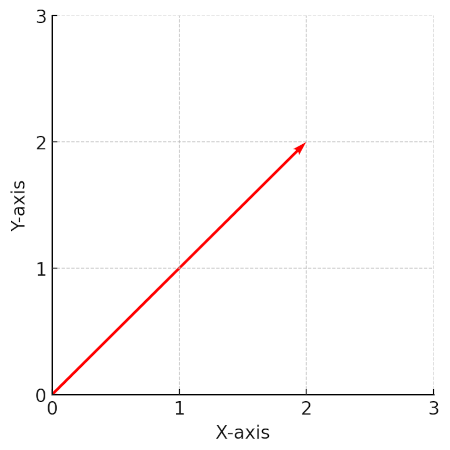
The norm defines the vector magnitude. In other words, the norm defines the length of the ‘arrow’ that goes from the origin up to the data point in space.
The Euclidean norm is defined as:
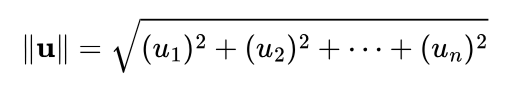
or
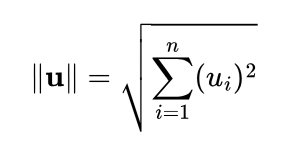
(“u” is for vector, the double bars for “norm”)
The norm is the square root of the sum of the squares of each component of the vector. If Pythagora’s theorem came to mind, you are on the right track, this is a direct derivation of it.
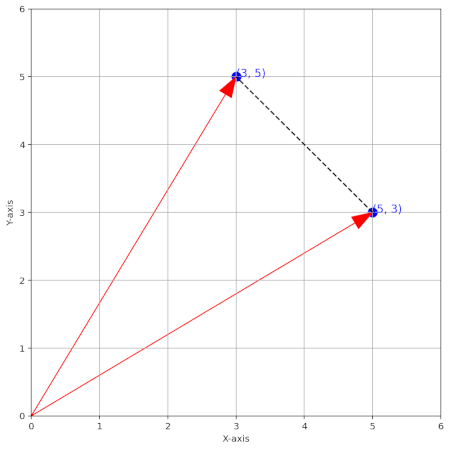
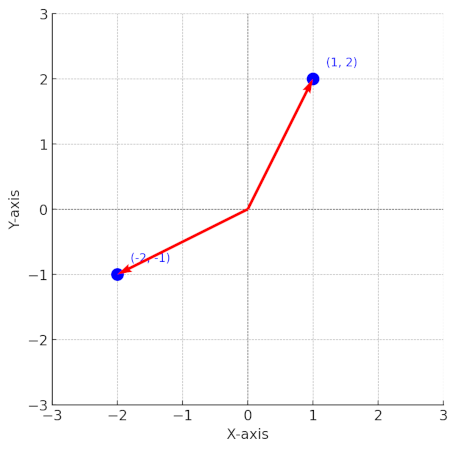
This is the “Euclidean distance” (commonly used with embedding models for instance). It’s just Pythagorean theorem: the vector norms (magnitudes) are catheti and the distance is the computed hypotenuse.
(the Pythagorean theorem works on n-dimensional spaces!)
So a vector is not an arrow?
That’s right, a vector is not necessarily an arrow. A vector does not have a magnitude by definition. It becomes one when ‘attaching’ a norm to the vector space (as demonstrated in the previous section).
I lost count how many times I’ve seen vectors being defined as:
A vector is an object that has both a magnitude and a direction.
Pointing out that such definition is incorrect it’s a bit of a nitpick, most of the time (especially in physics) it’s a given that the vector will be an arrow.
Internal product
An internal product it’s a function that takes two vectors and gives back a single scalar. Such scalar is supposed to measure how ‘aligned’ or ‘similar’ they are.
The standard internal product picked up for Euclidean spaces is the dot product:
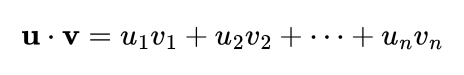
or
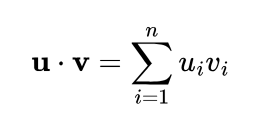
By calculating the dot product we can infer its direction. If dotproduct(u, v) = 0, the vectors are orthogonal (90°
angle):
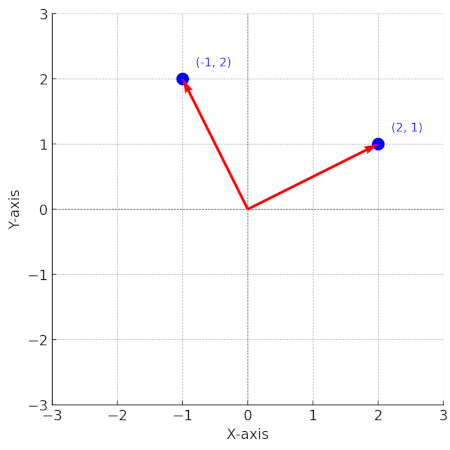
If dotproduct(u, v) > 0, the vectors have similar directions (acute angle, < 90°):
If dotproduct(u, v) < 0, the vectors have opposite directions (obtuse angle, > 90°)